Omega language

An ω-language is a set of infinite-length sequences of symbols.

1 Formal definition
2 Operations
3 Distance between ω-words
4 Important subclasses
5 Bibliography

Formal definition

Let Σ be a set of symbols (not necessarily finite). Following the standard definition from formal language theory, Σ^* is the set of all finite words over Σ. Every finite word has a length, which is, obviously, a natural number. Given a word w of length n, w can be viewed as a function from the set {0,1,...,n-1} → Σ. The infinite words, or ω-words, can likewise be viewed as functions from 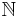$\mathbb{N}$ to Σ, with the value at i giving the symbol at position i. The set of all infinite words over Σ is denoted Σ^ω. The set of all finite and infinite words over Σ is sometimes written Σ^∞.

Thus, an ω-language L over Σ is a subset of Σ^ω.

Operations

Some common operations defined on ω-languages are:

Intersection and union. Given ω-languages L and M, both L ∪ M and L ∩ M are ω-languages.
Left catenation. Let L be an ω-language, and K be a language of finite words only. Then K can be catenated on the left only to L to yield the new ω-language KL.
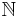Omega (infinite iteration). As the notation hints, the operation ( $\cdot$ )^ω is the infinite version of the Kleene star operator on finite-length languages. Given a formal language L, L^ω is the ω-language of all infinite sequence of words from L; in the functional view, of all functions $\mathbb{N}$ →L.
Prefixes. Let w be an ω-word. Then the formal language Pref(w) contains every finite prefix of w.
Limit. Given a finite-length language L, an ω-word w is in the limit of L if and only if Pref(w) ∩ L is an infinite set. In other words, for an arbitrarily large natural number n, it is always possible to choose some word in L, whose length is greater than n, and which is a prefix of w. The limit operation on L can be written L^δ or $\vec{L}$ .

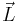Distance between ω-words

The set Σ^ω can be made into a metric space by definition of the metric d:Σ^ω × Σ^ω → R as:

if w and v share any finite prefix, then d(w,v)= inf {2^-|x| : x in Σ^*, and x in both Pref(w) and Pref(v) }.

otherwise d(w, v)=1

where |x| is interpreted as "the length of x" (number of symbols in x), and inf is the infimum over sets of real numbers. If w=v, they have no longest finite prefix, and d(w,v)=0; it can be shown that d satisfies all the other necessary properties of a metric.

Important subclasses

The most widely-used subclass of the ω-languages is the set of ω-regular languages, which enjoy the useful property of being recognizable by Büchi automata; thus the decision problem of ω-regular language membership is decidable and fairly straightforward to compute.

Bibliography

Perrin, D. and Pin, J-E. "Infinite Words Automata, Semigroups, Logic and Games". Pure and Applied Mathematics Vol 141, Elsevier, 2004.
Staiger, L. "ω-Languages". In G. Rozenberg and A. Salomaa, editors, Handbook of Formal Languages, Volume 3, pages 339-387. Springer-Verlag, Berlin, 1997.
Thomas, W. "Automata on Infinite Objects". In Jan van Leeuwen, editor, Handbook of Theoretical Computer Science, Volume B: Formal Models and Semantics, pages 133-192. Elsevier Science Publishers, Amsterdam, 1990.